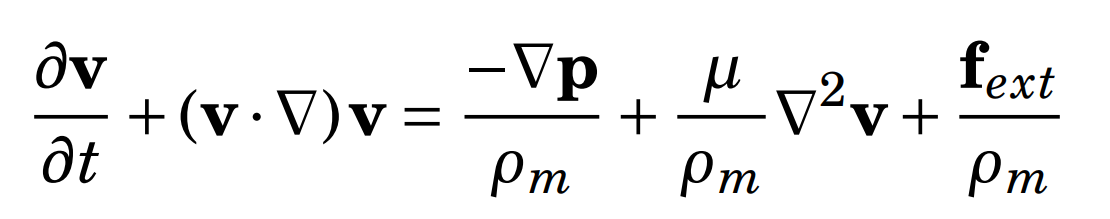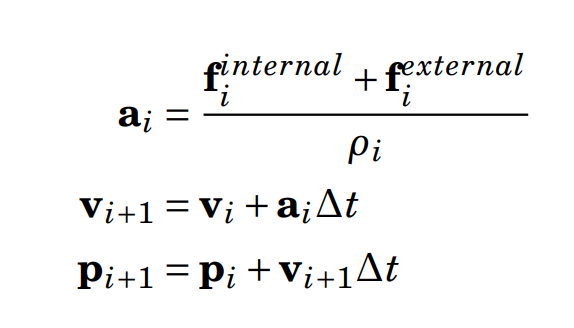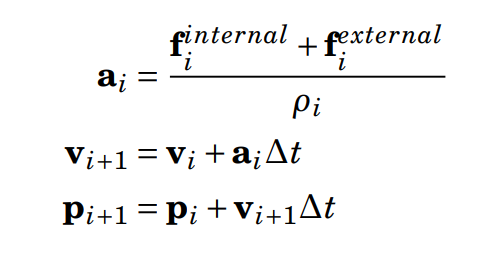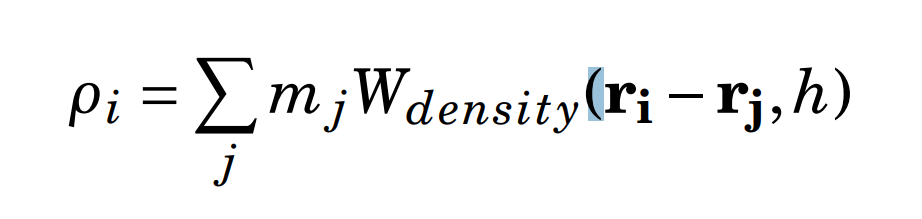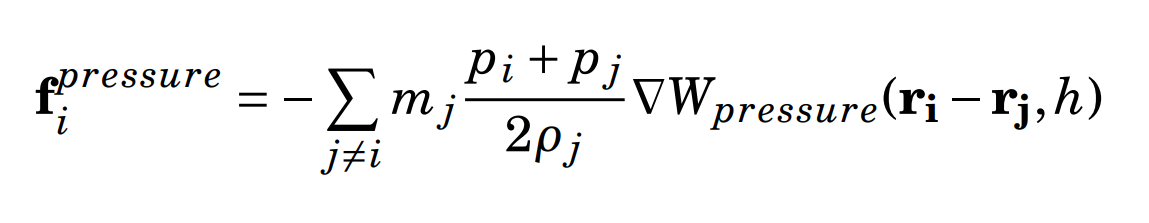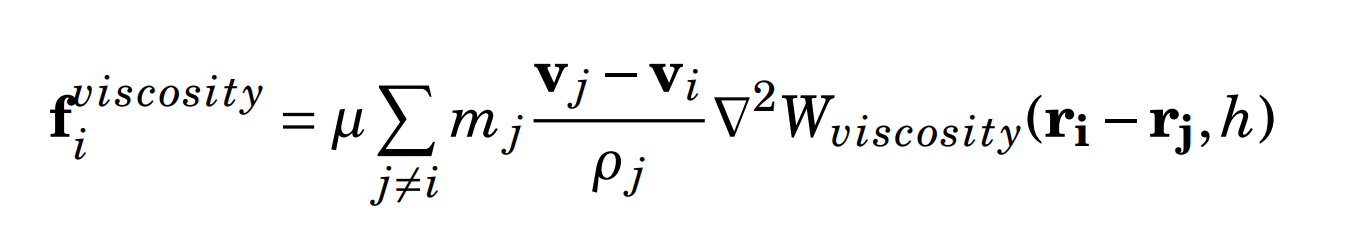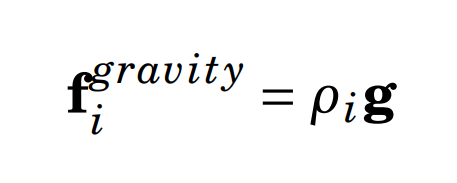GPU - Smoothed Particle Hydrodynamics

About Smoothed Particle Hydrodynamics

The objective of this exercise was to use a combination of CUDA kernels to complete a larger task. To do so, I had to introduce synchronization points, resolve conflicts for common memory addresses and build optimization structures.

Spatial Data Structure

While it would be possible to test all pairs of particles for influences, it is not very efficient. The O(n²) complexity of this approach makes it very slow for higher particle counts. To speed up the detection process, usually a spatial data structure is used. Instead of testing all possible pairs of particles, each particle is first inserted into the spatial data structure which then provides a way to quickly find only the particles that currently reside within a particular region.
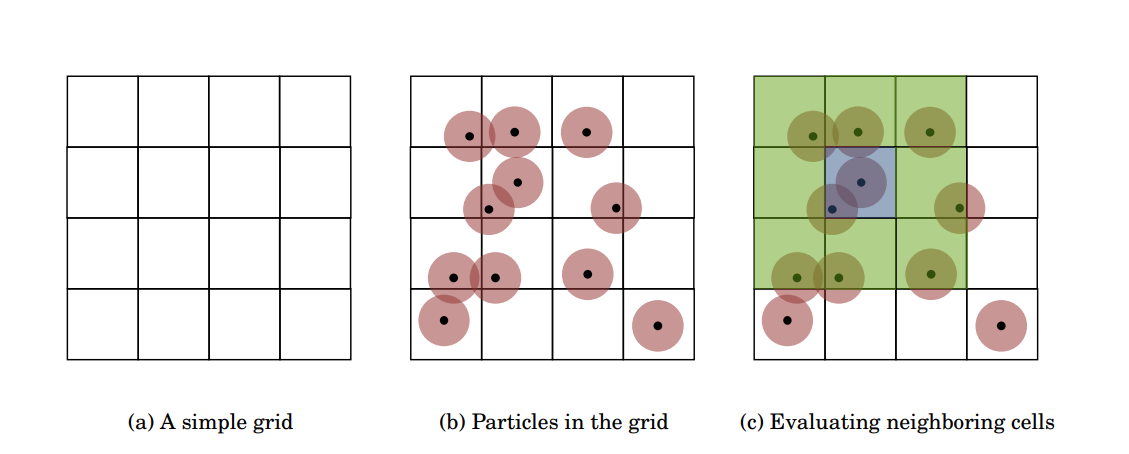
We used a simple, uniform grid data structure by following these steps:
1. Launch a kernel for each particle. Compute the grid cell the particle currently is in and use atomicAdd to count the number of particles in each cell (cellCount).
2. Run a prefix sum (scan) on cellCount to get memory offsets for each cell.
3. Launch another kernel similar to the first, again using atomicAdd for counting the particles in each cell. Use the return value of the atomic operation to determine the particles position within the cell. Combine this offset with the offset from the prefix sum to get the index in a global array grid.
4. Launch a kernel for each particle. Again compute the particle’s cell, look up the memory offset for this cell from the prefix sum result and iterate through all particles in the same cell to determine possible collisions. As particles can be at cell boundaries and thus reach into neighboring cells, extend the search to all 26 neighboring cells.

Implementation detail

Smoothed particle hydrodynamics (SPH) builds upon the Navier-Stokes equation which looks as follows:

where v is the velocity, p is the pressure, µ is the viscosity, f_ext are external forces, e. g., due to gravity, and ρ_m is the mass density, defined as ρ_m = ρm, where m is the mass.

SPH approaches the numerical integration of the Navier-Stokes equation by the simulation of particles. Each particle represents a sample in the space that is being simulated. It also carries fluid properties, such as mass, velocity, density, temperature, etc. For our simulation, we associate each particle with a constant mass. We will not simulate temperature or more complex properties. It must be possible to reconstruct the fluid properties for the entire space that is being simulated from the simulated particles. To this aim, the particle properties are smoothed out using a smoothing function W(r,h). The kernel support h can be seen as the area of influence and r denotes the positional difference between two particles. In this exercise we will use three smoothing kernels 1, 2, 3 for the SPH simulation with kernel support h equal to four times the particle radius:

To solve the Navier-Stokes equation, it is necessary to compute the acceleration a particle experiences at a given time step ∂v/∂t and update the particles position accordingly (considering the influence of (v * ∇)v). To this aim, we have to compute the acceleration for each particle as defined on the right-hand side of the equation. We can achieve this by carrying out the following steps:

1. Compute density ρ for each particle
2. Calculate the internal pressure forces f_pressure from the densities
3. Compute internal viscosity forces f_viscosit y and the dissipation forces f_dissipation
4. Compute the external forces gravity f_gravit y and buoyancy f_buoyancy
5. Resolve collisions with obstacles
Then, we can perform the integration step by using Semi-implicit Euler integration.

We can then perform the integration step by using Semi-implicit Euler 4 integration:

More detail

Density Computing the density ρi for each particle location ri is straightforward:

where j runs over all particles. Since the kernels are 0 for ||r_i −r_j|| > h, we only need to consider particles that are at most h away from particle i. You can use the spatial data structure described later to limit your computations to these particles. You will have to compute the density in a separate kernel launch beforehand, as particles will require the surrounding density for further computations.

Pressure The pressure p can be derived from the density ρ as follows:
p = k(p-p₀)
where k is a spring constant that defines how compressible a fluid behaves and ρ₀ is the natural density of the fluid, i. e., a density at which no pressure arises. Ideally, we would like to use a high k (ideally the square of the speed of sound). This can easily lead to instabilities (would require very small time steps). Thus, we have to work with a lower k in practice.
To compute the pressure gradients, it is necessary to estimate the pressure difference between all influencing particle pairs. This can be done using the symmetric difference estimator.
This results in the following formula for the velocity change due to pressure:


Viscosity and Dissipation Viscosity can simply be modelled as particles transferring their velocity v to surrounding particles:

where µ is the viscosity coefficient of the fluid.

Gravity and Buoyancy Fluid particles experience body force due to gravity g:

Buoyancy is an upward force opposing gravity based on density differences inside the fluid. Depending on the fluid that surrounds a fluid particle, the particle can either be dragged down or be spilled up. This behaviour can be modelled using the particle densities:
where b is the buoyancy coefficient and ρavg is the average surrounding density. The surrounding density is computed by averaging the density values of all particles which lie within the kernel support h of the current particle.

And yeeep.. If you got to here, your head probably just exploded like mine did when I first saw all of this. It was very hard and easy at the same time to implement. Hard because one little accident in the formulas and nothing worked anymore. Easy because all the euquations where given and explained. In the end I got a great result! :)

Contact me

Please reach me at marc.kletz@hotmail.com if you want to get in touch.